[Algorithm] 최소신장트리(MST) - Prim
하나의 정점에서 연결된 간선들 중에 하나씩 선택하면서 MST를 만들어가는 방식
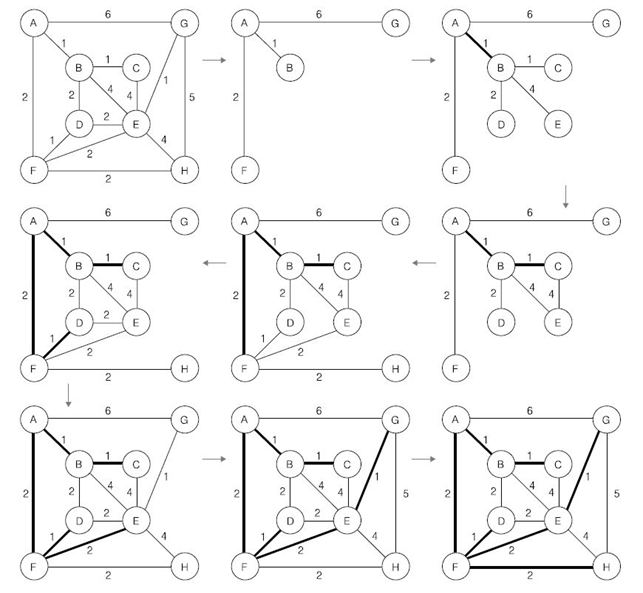
- 임의의 정점을 하나 선택
- 선택한 정점과 인접하는 정점들 중의 최소 비용의 간선이 존재하는 정점을 선택
- 모든 정점이 선택될 때까지 1, 2 과정을 반복
code
Edge
public class Edge {
int adjvertex; // 간선의 다른쪽 끝 정점
int weight; // 간선의 가중치
public Edge(int v, int wt) {
adjvertex = v;
weight = wt;
}
}PrimMST
import java.util.List;
public class PrimMST {
int N; // 그래프 정점의 수
List<Edge>[] graph;
public PrimMST(List<Edge>[] adjList) { // 생성자
N = adjList.length;
graph = adjList;
}
public int[] mst (int s) { // Prim 알고리즘,s는 시작정점
boolean[] visited = new boolean[N]; // 방문된 정점은 true로
int[] D = new int[N];
int[] previous = new int[N]; // 최소신장트리의 간선으로 확정될 때 간선의 다른 쪽 (트리의)끝점
for(int i = 0; i < N; i++){ // 초기화
visited[i] = false;
previous[i] = -1;
D[i] = Integer.MAX_VALUE; // D[i]를 최댓값으로 초기화
}
previous[s] = 0; //시작정점 s의 관련 정보 초기화
D[s] = 0;
for(int k = 0; k < N; k++){ // 방문안된 정점들의 D 원소들중 에서 최솟값가진 정점 minVertex 찾기
int minVertex = -1;
int min = Integer.MAX_VALUE;
for(int j=0;j<N;j++){
if ((!visited[j])&&(D[j] < min)){
min = D[j];
minVertex = j;
}
}
visited[minVertex] = true;
for (Edge i : graph[minVertex]){ // minVertex에 인접한 각 정점의 D의 원소 갱신
if (!visited[i.adjvertex]){ // 트리에 아직 포함 안된 정점이면
int currentDist = D[i.adjvertex];
int newDist = i.weight;
if (newDist < currentDist){
D[i.adjvertex] = newDist; // minVertex와 연결된 정점들의 D 원소 갱신
previous[i.adjvertex] = minVertex; // 트리 간선 추출을 위해
}
}
}
}
return previous; // 최소신장트리 간선 정보 리턴
}
}수행시간
Prim 알고리즘은 N번의 반복을 통해 minVertex를 찾고 minVertex에 인접하면서 트리에 속하지 않은 정점에 해당하는 D 의 원소 값을 갱신
PrimMST 클래스에서는 minVertex를 배열 D에서 탐색하는 과정에서 $O(N)$ 시간이 소요되고, minVertex에 인접한 정점들을 검사하여 D의 해당 원소를 갱신하므로 $O(N)$ 시간이 소요된다. 따라서 총 수행시간은
$$
N\times(O(N) +O(N)) = O(N^2)
$$
Reference
『IT CookBook, 자바로 배우는 쉬운 자료구조』, 이지영 집필, 한빛아카데미(2008)
『SW 문제해결 응용 - 구현 - 그래프의 최소 비용 문제』
https://swexpertacademy.com/main/learn/course/subjectDetail.do?subjectId=AV3GBeD6AF4BBARB#
'Algorithm' 카테고리의 다른 글
| [Algorithm] 최소신장트리(MST) (0) | 2019.11.10 |
|---|---|
| [Algorithm] 최소신장트리(MST) - Kruskal (0) | 2019.11.10 |
| PowerSet(부분집합) (0) | 2019.10.19 |
| Disjoint-Set (서로소 집합) (0) | 2019.10.15 |
| CaseOfNumber - 조합 & 중복조합 &순열 & 중복순열 (0) | 2019.10.09 |