계수정렬(Counting Sort)
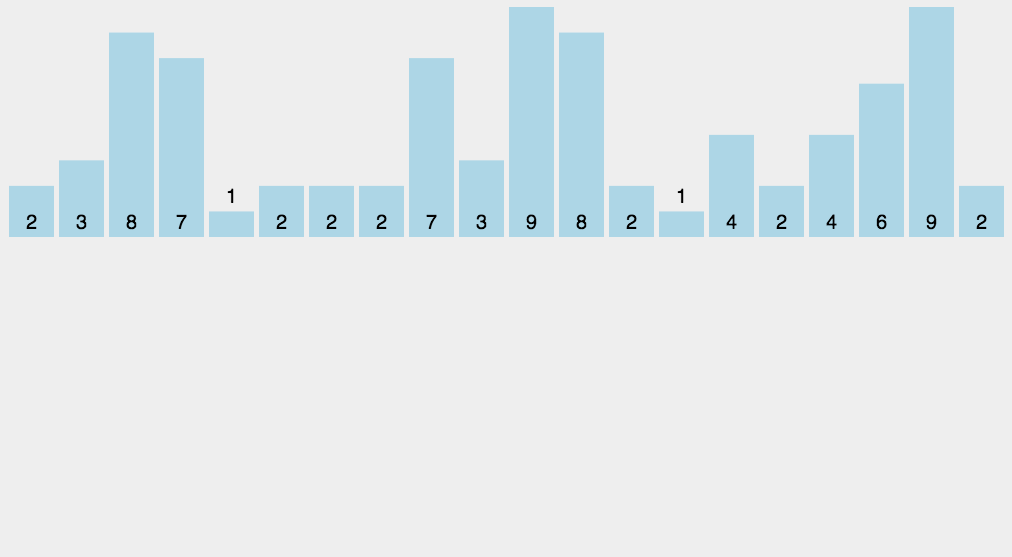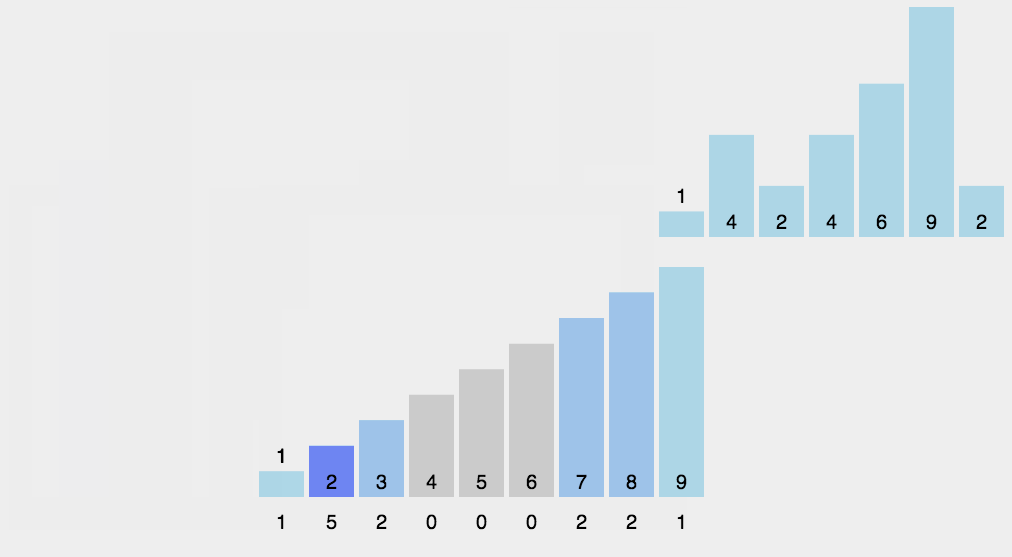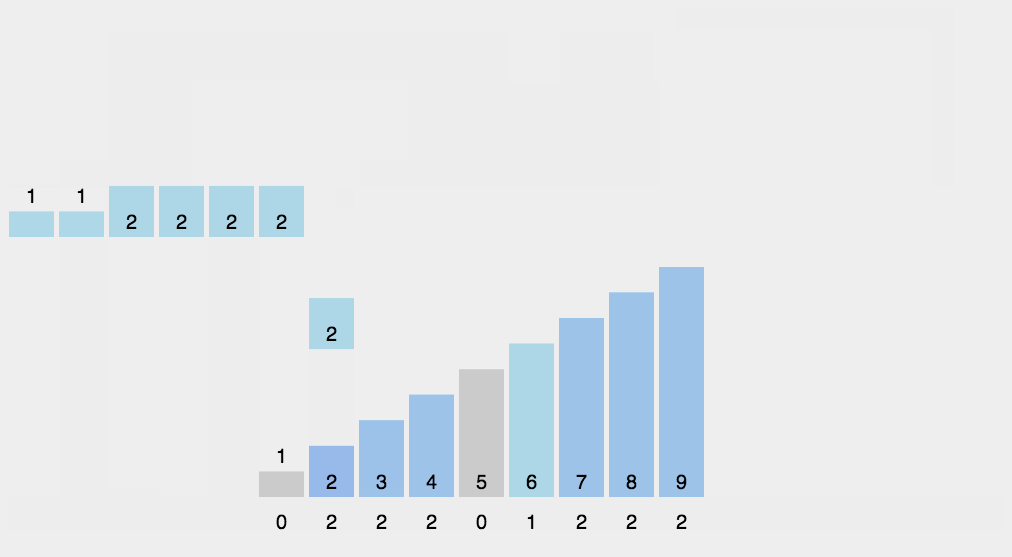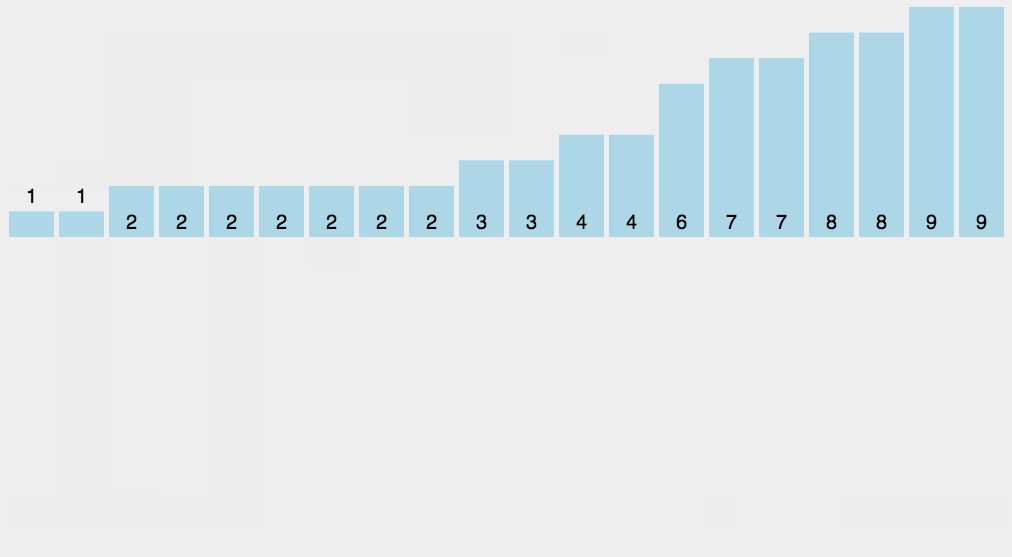
개념
Counting Sort는 숫자들간 비교를 하지 않고 정렬을 하는 알고리즘이다. 각 숫자가 몇개 있는지 개수를 세어 저장한 후에 정렬하는 방식이다.
로직
- 정렬하고자 하는 배열의 최대값을 구한다.
- 최대값 크기의 배열에 각 원소를 순회하며 해당 값이 몇개인지 저장한다.
- 저장된 데이터를 순서대로 출력한다.
코드
CountingSort.java
package Algorithm;
import java.util.Arrays;
import java.util.Random;
public class CountingSort {
static final int N = 10;
public static void main(String[] args) {
Random random = new Random(); // 랜덤함수를 이용
int[] arr = new int[N];
for (int i = 0; i < N; i++) {
arr[i] = random.nextInt(100); // 0 ~ 99
}
System.out.println("정렬 전: " + Arrays.toString(arr));
countingSort(arr);
System.out.println("정렬 후: " + Arrays.toString(arr));
}
private static void countingSort(int[] arr) {
// 최대값 구하기
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (max < arr[i])
max = arr[i];
}
int[] counting = new int[max + 1]; // 카운팅 배열
for (int i = 0; i < N; i++) {
counting[arr[i]]++;
}
int index = 0;
for (int i = 0; i < counting.length; i++) {
while (counting[i]-- > 0) {
arr[index++] = i;
}
}
}
}
console
정렬 전: [71, 89, 39, 93, 92, 27, 19, 15, 74, 76]
정렬 후: [15, 19, 27, 39, 71, 74, 76, 89, 92, 93]시간복잡도
$O(N+K)$ : 이때, $K$는 배열의 최대값이다.
장점
- $O(N)$의 매우 빠른 속도로 정렬이 가능하다.
단점
- 음수나 실수는 정렬할 수 없다.
- 추가적인 메모리 공간이 필요하며 값의 분포의 따라 메모리 낭비가 심할 수 있다.
'Algorithm' 카테고리의 다른 글
| 기수정렬(Ridix Sort) (1) | 2020.07.19 |
|---|---|
| 힙 정렬(Heap Sort) (0) | 2020.07.19 |
| 병합정렬(Merge sort) (0) | 2020.07.19 |
| 퀵정렬(Quick Sort) (0) | 2020.07.19 |
| 선택정렬(Selection Sort) (0) | 2020.07.19 |